Kalman Filter Basics

Kalman Filter Model and Understanding of P, Q, and R #

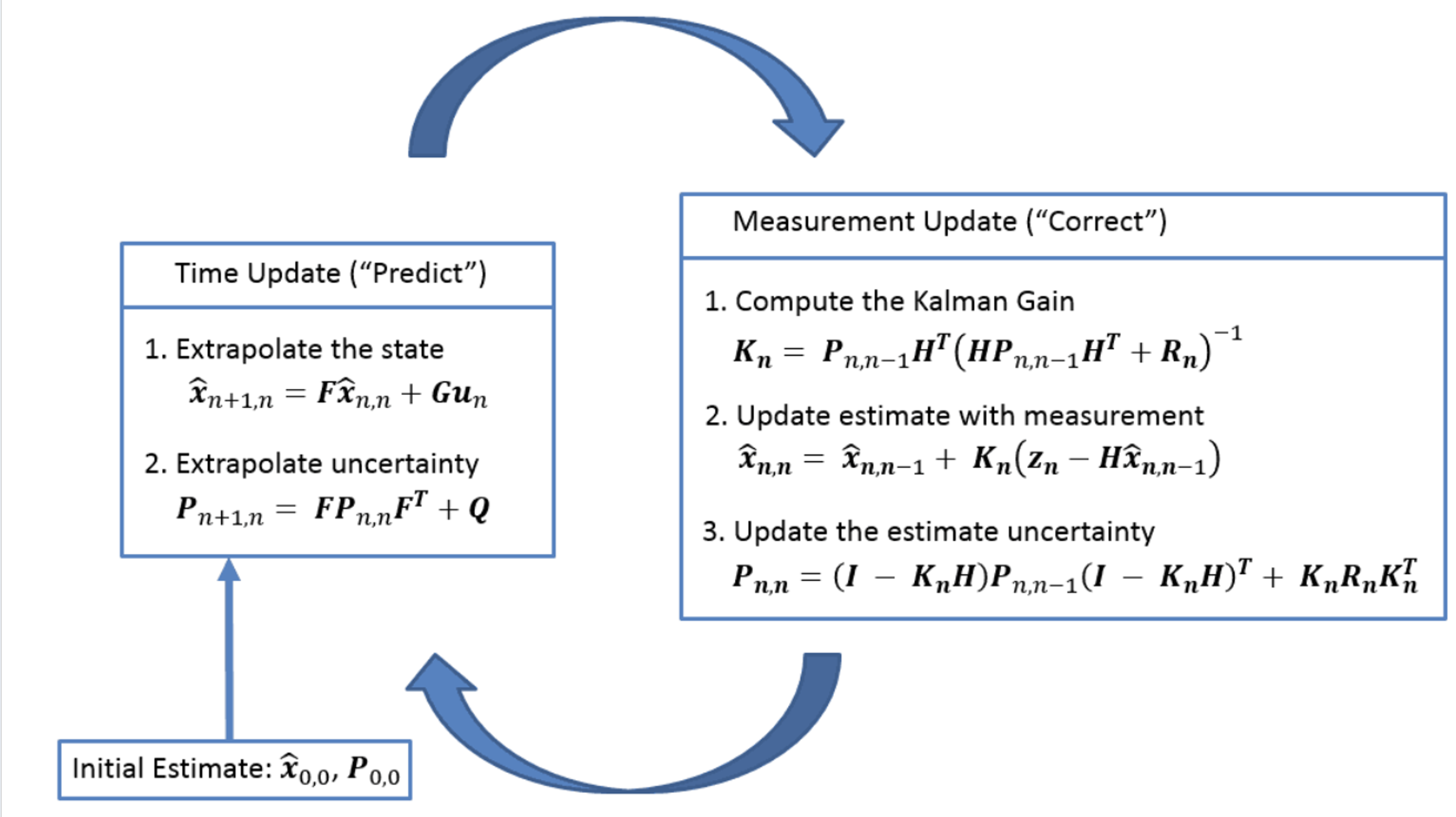
Prediction Step:

1. Predicted State Estimate: $$\hat{x}{k|k-1} = F{k-1}\hat{x}{k-1|k-1} + B{k-1}u_{k-1}$$
2. Predicted Covariance Estimate: $$P_{k|k-1} = F_{k-1}P_{k-1|k-1}F_{k-1}^T + Q_{k-1}$$

Update Step:

1. Innovation or Measurement Residual:
   $$y_k = z_k - H_k\hat{x}_{k|k-1}$$
2. Innovation Covariance: $$S_k = H_kP_{k|k-1}H_k^T + R_k$$
3. Kalman Gain: $$K_k = P_{k|k-1}H_k^TS_k^{-1}$$
4. Updated State Estimate: $$\hat{x}{k|k} = \hat{x}{k|k-1} + K_ky_k$$
5. Updated Covariance Estimate: $$P_{k|k} = (I - K_kH_k)P_{k|k-1}$$

Kalman Filter Model Components #

• State Vector: $x$

  • Represents the quantities the filter is estimating (e.g., position and velocity).

• State Transition Matrix: $F$

  • Models how the state evolves from one time step to the next.

• Control Input Model: $B$ (if control inputs are used)

  • Models how control inputs (e.g., acceleration) affect the state.

• Control Vector: $u$

  • Represents control inputs to the system.

• Measurement Vector: $z$

  • Represents the measurements used to update the state estimates.

• Measurement Function: $H$

  • Maps the state space into the measurement space.

• Process Noise Covariance Matrix: $Q$

  • Represents the uncertainty in the process model.

• Measurement Noise Covariance Matrix: $R$

  • Represents the expected noise or errors in the measurements.

• State Covariance Matrix: $P$

  • Represents the estimated accuracy of the state estimates (uncertainty in the state estimates).

Understanding of P, Q, and R #

Kalman Filter Model #

• State Vector: $x$

  • Represents the quantities the filter is estimating (e.g., position and velocity).

• State Transition Matrix: $F$

  • Models how the state evolves from one time step to the next.

• Control Input Model: $B$ (if control inputs are used)

  • Models how control inputs (e.g., acceleration) affect the state.

• Control Vector: $u$

  • Represents control inputs to the system.

• Measurement Vector: $z$

  • Represents the measurements used to update the state estimates.

• Measurement Function: $H$

  • Maps the state space into the measurement space.

• Process Noise Covariance Matrix: $Q$

  • Represents the uncertainty in the process model.

• Measurement Noise Covariance Matrix: $R$

  • Represents the expected noise or errors in the measurements.

• State Covariance Matrix: $P$

  • Represents the estimated accuracy of the state estimates (uncertainty in the state estimates).

Understanding of $P$, $Q$, and $R$ #

• Process Noise Covariance $(Q)$

  • Represents uncertainty in the process model or system dynamics.
  • Larger $Q$ implies less confidence in the model, or more inherent unpredictability.
  • In the prediction step, $Q$ is added to $P$ to account for the increase in uncertainty over time.

• Measurement Noise Covariance ($R$)

  • Quantifies the expected noise or errors in the sensor measurements.
  • Larger $R$ indicates less reliable measurements.
  • Influences the Kalman Gain $K$. Smaller $R$ increases $K$, making the filter more responsive to measurements.

• State Covariance Matrix ($P$)

  • Represents the filter’s current confidence in its state estimates.
  • Updated during both prediction and correction steps.
  • Smaller values in $P$ indicate higher confidence in the estimates.

Key Points #

• $Q$ adds uncertainty to $P$ in the prediction phase, acknowledging that the state becomes less certain over time without new measurements.
• $R$ affects the calculation of $K$ in the update phase. A smaller $R$ (trusting measurements more) increases $K$, leading to greater adjustment of the state estimate based on the current measurement.
• The Kalman Filter continuously adjusts the state estimate by balancing model predictions (with uncertainty $Q$) and measurement updates (with uncertainty $R$). The state covariance matrix $P$ encapsulates this balance at each step.